ST表
约 356 个字 70 行代码 预计阅读时间 2 分钟
RMQ (Range Minimum/Maximum Query)¶
区间最值的问题。
ST表¶
符合结合律且可重复贡献的信息查询
可重复贡献:交集不为空的区间合并,不影响结果
倍增思想
时间复杂度¶
O(nlogn) 预处理
O(1) 查询
空间复杂度¶
O(nlogn)
预处理¶
我们建立一个MAX[maxn][21]数组来储存以当前数组为起点的,连续2^n的范围内的最大值,其中MAX[maxn][0]即为2 ^ 0 = 1范围内的最大值,即数字本身。
然后使用动态规划来将MAX数组处理。
int MAX[maxn][21];
inline void init(int n){
for(int j = 1;j <= 21;j++){
for(int i = 1;i + (1 << j) - 1 < n;i++){
MAX[i][j] = max(MAX[i][j-1], MAX[i + (1 << (j-1))][j-1]);
}
}
}
这个动态规划可以用下面这个图来解释
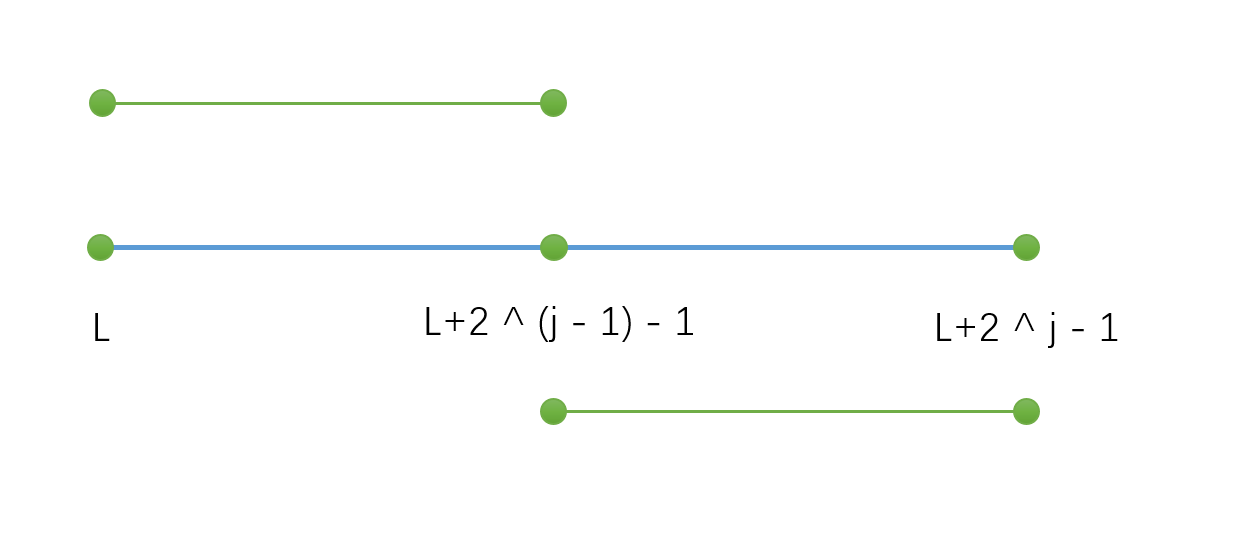
整段的最大值是左右两段其中之一的最大值。
查询¶
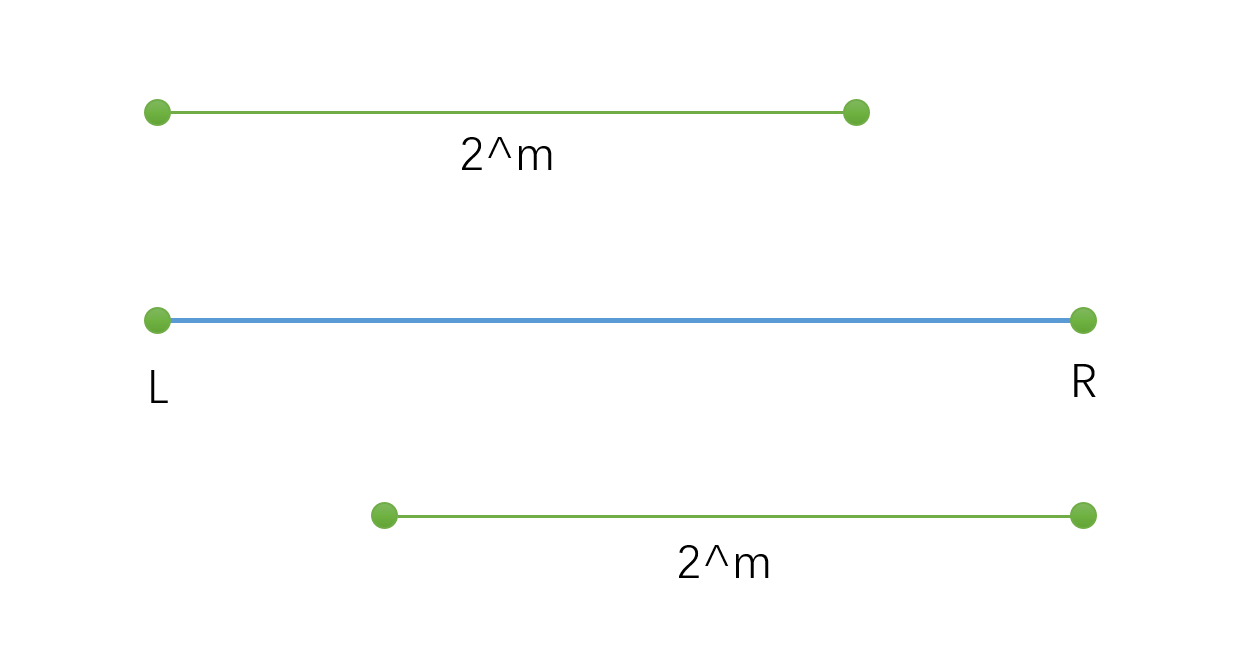
查询和上面的思路一样,因为我们已经找出来了以每个数字为起点,长度为2^n的序列的最大值,因此我们只需要将整个区间分成两个区间的并集即可,为了保证两个小区间一定包含了全部区间,两个小区间需要尽量大,最好是都是2^n长。
int lg[maxn];//预先计算lg,如果觉得麻烦可以直接用log2()函数
int query(int l, int r){
int m = lg[l - r + 1] - 1;//使用与lca同样的方法将全部的lg算出来,减小常数,注意有偏移要减回来
return max(MAX[l][m], MAX[r - (1 << m) + 1][m]);
}
for(int i = 1;i < n;i++){
lg[i] = lg[i-1] + (1 << lg[i - 1] == i);//偏移了1,
}
区间长度为2 ^ m长,这是[L,r]内最长的次方数,也是最长的2^n长度。
模板题代码¶
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = 1e5 + 5;
int f[maxn][21];
int lg[maxn];
inline void init(int n){
for(int i = 1;i <= n;i++){
lg[i] = lg[i-1] + (1 << lg[i-1] == i);
}
for(int j = 1;j <= 21;j++){
for(int i = 1;i + (1 << j) - 1 <= n;i++){
f[i][j] = max(f[i][j-1], f[i + (1 << (j - 1))][j-1]);
}
}
}
inline int query(int l, int r){
int mid = lg[r - l + 1] - 1;
return max(f[l][mid], f[r - (1 << mid) + 1][mid]);
}
signed main(void){
int n, m;
scanf("%d %d",&n, &m);
for(int i = 1;i <= n;i++)scanf("%d",&f[i][0]);
init(n);
for(int i = 1;i <= m;i++){
int l, r;
scanf("%d %d",&l, &r);
printf("%d\n",query(l,r));
}
return 0;
}
板子¶
__lg是一条指令就能完成,所以不需要预处理log数组
把小的那一维放在前面会更cache友好
const int N = 5e4 + 3;
const int M = __lg(N) + 1;
namespace SparseTable
{
int st[M][N];
void init(int n)
{
int m=__lg(n);
memcpy(st[0],a,sizeof(int)*(n+1));
for (int i = 1; i <=m; ++i)
{
for (int j = 1; j + (1 << i) - 1 <= n; ++j)
st[i][j] = min(st[i-1][j], st[i-1][j + (1 << (i - 1))]);
}
}
int query(int l, int r)
{
int s = __lg(r - l + 1);
return min(st[s][l], st[s][r - (1 << s) + 1]);
}
};